A framework for designing problem solving task for secondary school mathematics classroom
DOI:
https://doi.org/10.23917/jramathedu.v8i2.3137Keywords:
Mathematical Problem Solving, Mathematics Instruction, Mathematics Education, Teaching Through Problem SolvingAbstract
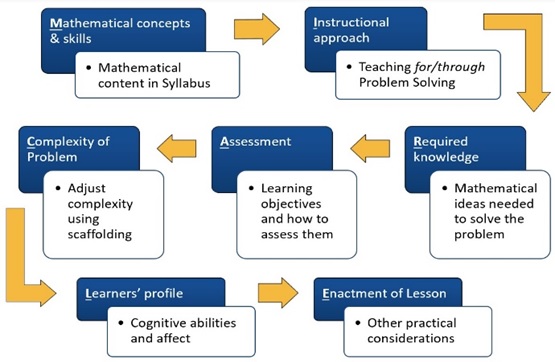
Although problem solving has been playing a critical role in the teaching and learning of mathematics in K-12 in many countries in the world, anecdotal evidence from mathematics classrooms shows that teachers are still facing challenges in designing mathematical tasks on problem solving for classroom instruction. Despite the effort of several existing research studies on enacting problem solving in the mathematics classroom, the guiding principles for designing problem solving tasks remain largely unexplored, thus teachers are left without being empowered to design their own problem solving tasks. The objective of this paper is to provide a comprehensive framework on designing problem solving tasks through a list of interrelated guiding principles. The proposed framework, which we name MIRACLE, foreground seven key considerations which mathematics educators should take into consideration when designing a task for a problem solving lesson: Mathematical content, method of Instruction, Required knowledge, Assessment, Complexity of problem, Learner’s profile, and Enactment of lesson. This paper also provides two exemplars on how the framework could be used to design mathematical tasks for problem solving through problem solving
References
Anderson, L. W., & Krathwohl, D. R. (Eds.). (2001). A taxonomy for learning, teaching and assessment: A revision of Bloom’s taxonomy of educational objectives (complete ed.). Longman.
Brookhart, S. M., & McMillan, J. H. (2020) Classroom assessment and educational measurement. Routledge.
Butt, G. (2008). Lesson planning (3rd ed.). Continuum International Publishing Group.
Chamberlin, S. A. (2019). The Construct of Affect in Mathematical Modeling. In Chamberlin, S. A. & Sriraman, B. (Eds.), Affect in mathematical modeling. Springer.
Chamberlin, S. A., & Parks, K. (2020). A comparison of student affect after engaging in a mathematical modeling activity. International Journal of Education in Mathematics, Science and Technology, 8(3), 177-189.
Choy, B. H. (2018). From Task to Activity: Noticing Affordances, Design, and Orchestration. In P. C. Toh, & B. L. Chua (Eds.), Mathematics instruction: Goals, tasks and activities (pp. 11-31). World Scientific.
De Lange, J. (2007). Large-scale assessment and mathematics education. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 1111 – 1142). Information Age Publishing.
Deng, Z., Gopinathan, S., & Lee, C. K. E. (2013). The Singapore Curriculum: Convergence, Divergence, Issues and Challenges. In Z. Deng, S. Gopinathan, & C. K. E. Lee (Eds.), Globalization and the Singapore Curriculum : From Policy to Classroom (pp. 263-275). Springer.
Depka, E. M. (2007). Designing assessment for mathematics. SAGE Publications.
Fan, L. H., & Zhu, Y. (2007). From convergence to divergence: The development of mathematical problem solving in research, curriculum, and classroom practice in Singapore. ZDM, 39(5), 491–501.
Gilmore, C., Göbel, S. M., & Inglis, M. (2018). An introduction to mathematical cognition. Routledge.
Hill, H., Rowan, B., & Ball, D. (2005). Effects of teachers’ mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42, 371-406.
Hino, K. (2018). Developing Interaction Toward the Goal of the Lesson in a Primary Mathematics Classroom. In Toh, P. C., & Chua, B. L. (Eds.), Mathematics instruction: Goals, tasks and activities (pp. 133-158). World Scientific.
Houff, S. (2012). Instructional alignment: Optimizing objectives, methods, and assessment for developing unit plans. Rowman & Littlefield.
Kaur, B., & Yeap, B. H. (2009). Mathematical Problem Solving in Singapore Schools. In B. Kaur, B. H. Yeap & M. Kapur (Eds.), Mathematical problem solving (pp. 1-13). World Scientific.
Kaur, B., Tay, E. G., Tong, C. L., Toh, T. L., & Quek, K. S. (2021). The Instructional Core That Drives the Enactment of the School Mathematics Curriculum in Singapore Secondary Schools. In B. Kaur & Y. H. Leong (Eds.), Mathematics Instructional Practices in Singapore Secondary Schools (pp. 45-59). World Scientific.
Krantz, S.G. (1997). Techniques of problem solving. American Mathematical Society.
Leong, Y. H., Tay, E. G., Toh, T. L., Quek, K. S., Toh, P. C., & Dindyal, J. (2016). Infusing Mathematical Problem Solving in the Mathematics Curriculum: Replacement Units. In P. Felmer, E. Pehkonen, & J. Kilpatrick (Eds.), Posing and Solving Mathematical Problems: Advances and New Perspectives (pp. 309-325). Springer.
Lester, F. K. (1983). Trends and issues in mathematical problem-solving research. In R. Lesh & M. Landau (Eds.), Acquisition of mathematical concepts and processes (pp. 229-261). Academic Press.
Lester, F. K., & Charles, R. (2003). Teaching Mathematics Through Problem Solving: Pre-K–Grade 6. Reston, National Council of Teachers of Mathematics.
Mason, J., & Johnston-Wilder, S. (2006). Designing and using mathematical tasks. Tarquin Publications.
Matlin, M. W. (2014). Cognitive psychology (8th ed.). John Wiley & Sons.
Piaget, J. (1952). The origins of intelligence in children. (M. Cook, Trans.). Norton.
Polya, G. (1945). How to solve it. Princeton University Press.
Schoenfeld. (1983). Problem solving in the mathematics curriculum : A report, recommendations, and an annotated bibliography. Mathematical Association of America, Committee on the Teaching of Undergraduate Mathematics.
Schoenfeld, A. (1985). Mathematical problem solving. Academic Press.
Schroeder, T., & Lester, F. (1989). Developing understanding in mathematics via problem solving. In P. Traffon & A. Shulte (Eds.), New directions for elementary school mathematics: 1989 yearbook (pp. 31-42). NCTM.
Stein, M. K., Grover, B. W., & Henningsen, M. (1996). Building Student Capacity for Mathematical Thinking and Reasoning: An Analysis of Mathematical Tasks Used in Reform Classrooms. American Educational Research Journal, 33(2), 455–488.
Stein, M., Kinder, D., Silbert, J., & Carnine, D. W. (2006). Designing Effective Mathematics Instruction: A Direct Instruction Approach (4th ed.). Pearson Merrill Prentice Hall.
Sweller, J., Ayres, P., & Kalyuga, S. (2011). Cognitive Load Theory. Springer.
Tan, O. S., Chye, Y. L. S., Lim, K. J., Chua, B. L., Tuckman, B. W., & Monetti, D. M. (2017). Educational psychology: An asia edition. Cengage Learning Asia Ltd.
Toh, T.L. (2010). Designing Mathematical Investigative Task. In Westbrook, M., Treeby, D., Sexton, C., Kilpatrick, A., McNamara, A., Huggan, M., Ross, M., Penney, J., Walsh, P., Bowden, J., Carroll, J., Ferguson, S., Lipson, D. (Ed.), New Curriculum. New Opportunities (pp. 36-45). Mathematical Association of Victoria.
Toh, T. L., Leong, Y. H., Tay, E. G., Quek, K. S., Toh, P. C., Dindyal, J., Ho, F. H., & Yap, R. A. S. (2013). Making mathematics more practical: Implementation in the schools. World Scientific.
Toh, T. L., Quek, K. S., Leong, Y. H., Dindyal, J., & Tay, E. G. (2011). Making mathematics practical: An approach to problem solving. World Scientific.
Toh, T.L., Quek, K.S., & Tay, E.G. (2008a). Mathematical Problem Solving - A New Paradigm. In Vincent, J., Pierce, R., Dowsey, J. (Eds.), Connected Maths: MAV Yearbook 2008 (pp. 356 - 365). Mathematical Association of Victoria.
Toh, T. L., Quek, K. S. & Tay, E. G. (2008b). Problem Solving in the Mathematics Classroom (Junior College). National Institute of Education & Association of Mathematics Educators.
Tomlinson, C. A. (2001). How to differentiate instruction in mixed-ability classrooms (2nd ed.). Association for Supervision and Curriculum Development.
Tomlinson, C. A. (2014). The Differentiated Classroom: Responding to the Needs of All Learners (2nd ed.). Association for Supervision and Curriculum Development.
Van de Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2019). Elementary and middle school mathematics: teaching developmentally (10th ed.). Pearson.
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes (M. Cole, V. John-Steiner, S. Scribner, & E. Souberman, Trans.). Harvard University Press.
Wong, K. Y. (2015). Effective mathematics lessons through an eclectic Singapore approach. Singapore: World Scientific.
Yeo, J. B. W. (2015). Development of a Framework to Characterise the Openness of Mathematical Tasks. International Journal of Science and Mathematics Education, 15(1), 175–191.
Downloads
Submitted
Published
How to Cite
Issue
Section
License
Copyright (c) 2023 Yu Xin NG, Tin Lam TOH

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


















