Using international large-scale assessment for learning: Analyzing U.S. students’ geometry performance in TIMSS

Abstract

The data from international large-scale assessments, such as The Trends in International Mathematics and Science Study (TIMSS), is often designed and used as an assessment of learning rather than an assessment for learning. This research employed TIMSS 2011 data, focusing on the geometric performance of fourth-grade students in the United States,  to demonstrate how large-scale assessments can be utilized qualitatively to identify students' learning challenges, providing valuable insights to inform geometry teaching practices. Using van Hiele’s levels of geometric thinking as a guiding framework, the 24 released geometry items were analyzed to identify students’ struggle points in geometry nationwide. Our analysis revealed that students performed well on tasks that were visual, contextually grounded, and had clearly defined manipulative expectations.. However, students needed further support to solve items requiring a deep understanding of geometrical concepts, such as finding the perimeter of a square. Additionally, students excelled at solving tasks involving the identification of relative positions of objects on a map and recognizing lines of symmetry in regular shapes. However, they struggled with measurement-related tasks. Our analysis also identified a range of item features that might cause difficulties that impacted the way students responded to these items. Instructional implications for elementary mathematics education are discussed.

INTRODUCTION

Geometry (inclusively, which includes measurement) is essential in itself and fundamental for other mathematics topics (Common Core State Standards Initiative, 2010; Lee & Lee, 2021; Lowrie & Logan, 2018; Yao, 2020), as well as pivotal significance for students participating in the modern workplace, especially in STEM fields (Cheng & Mix, 2014; Mix & Cheng, 2012; Tian et al., 2022; Wai et al., 2009). Tian et al. (2022) found that strong spatial skills in fourth grade could improve their chance of choosing STEM college fields after controlling math achievement and motivation, verbal achievement and motivation, and family background.

However, results from large-scale assessments Trends in International Mathematics and Science Study (TIMSS) and National Assessment of Educational Progress (NAEP) often show that U.S. students consistently lagged in geometry as compared to other mathematical content domains and their peers in other countries (Bokhove et al., 2019; Chen et al., 2021; Kloosterman & Lester, 2007; Provasnik et al., 2012). In general, research asserts that U.S. students struggle with geometrical topics (e.g., Fielker et al., 1979; Hershkowitz, 1987; Lehrer et al., 1998; Sinclair & Bruce, 2015; Wallrabenstein, 1973), which motivates mathematics educators and researcher to identify students’ struggle points to inform more responsive geometry education (e.g., Clements & Sarama, 2011; Fielker et al., 1979; Sinclair & Bruce, 2015).

Many qualitative studies have been conducted to assess students’ geometry learning, which can be used for students’ learning. This type of assessment is referred to as an assessment for learning, in which evidence about students’ knowledge, understanding, and learning difficulties is used to inform teachers’ instruction (Earl & Katz, 2006; Small, 2019). However, these results could not be generalized to a larger population, not mention . In other words, qualitative studies can help to identify students’ potential struggle points in learning geometry. Still,to what extent it represents the national populationed, which limits us from providing federal suggestions and explore cultural patterns.

To address this issue, a large-scale assessment is needed. However, analyses of large-scale assessments (e.g., TIMSS) are often used as an assessment of learning (e.g., Chen et al., 2021; Shapira-Lishchinsky & Zavelevsky, 2020) rather than assessing for learning. Assessment of learning is often referred to as summative assessment and serves for the grading or ranking purposes (Earl & Katz, 2006; Harlen, 2007), which barely concerns specific pedagogical implications for enriching students’ learning opportunities. Using TIMSS as an assessment of learning, researchers help the countries or regions to locate their mathematics education performance in the global context, which is especially useful for policymakers, administrators, and researchers to ascertain policy and curriculum reforms (Furner & Robison, 2004; Schmidt & McKnight, 1998; Schmidt et al., 2007).

But using TIMSS as an assessment of learning fails to provide fine-grained guidelines for supporting mathematics teachers’ instructional decision-making. For example, Provasnik et al. (2012) highlighted U mathematics performance in TIMSS 2011 data that “At grade 4, the United States was among the top 15” (p. iii) and “in comparison with other education systems, U.S. 4^thgraders performed better on average in number and data display than in geometric shapes and measures” (p. 14). While these results provide valuable insights into U.S. students' performance in geometry within a global context, they are insufficient for mathematics teachers or curriculum developers to implement meaningful changes to enhance students’ geometry learning opportunities. Simply knowing that U.S. fourth graders performed relatively poor in geometry does not offer enough guidance forteachers to adjust their instruction, especially without detailed information on how—and possibly why—students performed in each specific subtopic of geometry.

Therefore, researchers should aim to strike a balance that allows them to understand students' learning challenges on a broader scale, applicableto a national population. One approach is to use qualitative methods to analyze student performance on large-scale assessment items. This analysis can help identify specific subtopics in geometry that students find most or least challenging and uncover the underlying reasons (Liu, 2019). By doing so, educators and teachers accross the country can be better informed and provide appropriate instructions to support students’ geometric development. As such, this studyleverage the affordance of TIMSS data, which, in addition to making inferences related to the assessment of learning, examines data with a lens of assessment for learning. TIMSS items were analyzed to learn how to improve students’ geometry learning opportunities in effective and efficient ways. content analysiszoomin on the 24 released fourth-grade geometry items from TIMSS 2011van Hiele levels of each item to help identifying U.S. students’ areas of strengths and weaknesses in geometry. This study aims to answer the following two central research questions:

RQ1: What can be learned from the geometric items that U.S. students performed differently, with a focus on understanding the features of these items for supporting learning?

RQ2: How do U.S. students perform on each geometry subtopic, and what insights can be gained from the variations in performance regarding assessment for learning?

Learning difficulties of geometry and measurement

Research found that students’ struggle to understand geometric concepts, reasoning, and problem-solving in early grades is associated with their unpreparedness to learn learn other topics such as fractions (Liu & Jacobson, 2022) and abstract geometrical concepts and proof in high school (Clements & Battista, 1992). This calls for teachers to identify the areas where students struggle during the primary years so that they can create meaningful learning experiences for students to develop solid understanding of geometry (Zhou et al., 2021). Previous literature found that younger students’ geometric learning challenges cluster in the following three areas: shape classification, measurement, and transformation.

In geometry, shape classification is a complex area for students (e.g., Aslan & Arnas, 2007; Bernabeu et al., 2021; Clements et al., 1999; Guncaga et al., 2017; Walcott et al., 2009). Aslan and Arnas (2007) studied 3- to 6-year-old children’s recognition of geometric shapes and found that they performed better in identifying the typical forms of shapes (e.g., square with a horizontal base) and were distracted by the orientation or skewness of the shapes. Similarly, Bernabeu et al. (2021) investigated how 3rd-graders understand the concept of polygon and found students’ difficulties in classifying polygon due to their ability to identify relevant (side length, angle measure) and non-relevant (color or orientation of shape) attributes. Non-relevant attributes such as symmetry, concavity/convexity, number of sides, parallelism, and length of the sides in the triangles interrupted students’ understanding of definitions of a class of polygons, making it hard for students to recognize attributes that determine a class of figures (Bernabeu et al., 2021). In Walcott et al.’s (2009) analysis of an item that asked students to list the similarities and differences between the parallelogram and rectangle in the NAEP 4^th grade assessments in 1992 and 1996, they found that only 11% of 900 responded satisfactorily. Researchers conjectured that students’ understanding of shapes might be constructed based on their limited empirical experiences with (e.g., observing, touching, working with) shapes' attributes.

Measurement is another challenging area for students (e.g., Kamii & Kysh, 2006; Kim et al., 2017; Sevgi & Orman, 2020). Most students use measurement instruments or apply formulas (e.g., the perimeter of a square is four times the side length) to get the answer without understanding the conceptual underpinnings (Clements & Battista, 1992). For instance, students identify the square unit as the standard unit of area measurement and consider the concept of area as the number of square units (Barrett et al., 2017). There is a possibility that students might fail to solve tasks when the unit is triangular and rectangular, indicating difficulties related to space-covering or space-filling properties, which are critical aspects of understanding the concept of area (Barrett et al., 2017; Cullen & Barrett, 2020).

Researchers (e.g., Mammarella et al., 2012) observed that transformation was more challenging than shapes and measurement for students. Students needed help in understanding angles (Clements, 2004; Devichi & Munier, 2013; Uttal, 1996). They tended to believe that a right angle must orient to the right, and one ray of an angle must lie horizontally (Devichi & Munier, 2013; Fuys & Geddes, 1984; Mitchelmore, 1998). Changing an angle’s orientation challenged children’s reorganization of different types of angles (Devichi & Munier, 2013; Izard & Spelke, 2009). Researchers (e.g., Izard & Spelke, 2009; Spelke et al., 2010) hypothesized that students’ understanding of geometric topics, such as transformation, might be culturally mediated (e.g., an urban environment provided more opportunities for learning right angles). All these studies suggest that students struggle with conceptually understanding geometrical ideas, which could contribute to their performance in large-scale assessments (like TIMSS).

Van Hiele’s level as the analytical framework

Pierre Marie van Hiele and his wife, Dina van Hiele-Geldof (1984), identified five levels of thought in geometry. These original five levels are called the van Hiele levels. Mayberry (1983) described the five levels: Level 0 (visualization) indicates the ability to recognize figures by their appearance without perceiving their properties. Level 1 (analysis) entails identifying figures’ essential properties and seeing the shapes’ classes. At this stage, students do not see the relationships between the properties of diverse shapes and are likely to comprehend that all the properties of the shapes are of the same significance. Level 2 (informal deduction): Learners perceive the relationships between properties of different figures, create meaningful definitions, and understand class inclusions based on properties. Level 3 (deduction), learners comprehend the meaning of necessary and sufficient conditions for a geometric figure to understand the role of axioms and definitions and be able to construct mathematical proofs. Level 4 (rigor): Students understand the formal aspects of deduction and can function in non-Euclidean systems. Each of these levels has its characteristics and network of relations. A learner must master the level to achieve the higher level, emphasizing the importance of sequential and connected instruction as new ideas are developed based on prior knowledge of interrelated topics (van Hiele, 1984; van Hiele-Geldof, 1984). A learner’s progression from one level to the next level depends on the learner’s experiences with geometrical ideas.

Since the 1980s, researchers have validated the effectiveness of van Hiele levels in describing students’ development of geometric thinking (Fuys & Geddes, 1984; Mayberry, 1983; Wang & Kinzel, 2014). Others used van Hiele levels as an analytic framework to investigate whether the geometry curriculum aligns with the development of students’ geometric progression (e.g., Dingman et al., 2013; Newton, 2011; Zhou et al., 2022). This paper used van Hiele levels to reflect the geometric thinking required to solve a specific item. Given that TIMSS items addressed a range of topics, a modified version of the van Hiele model was adopted, as offered by the Ohio Department of Education (2018), which provided a detailed description of each of the levels concerning different sub-concepts covered in geometry curriculum (i.e., two- and three-dimensional shapes, transformations/location, and measurement [length, area, and volume]).

METHODS

Data source and gathering procedure

This study utilizes large-scale assessment data (using TIMSS 2011 data as a showcase) and employs descriptive statistics and content analysis methods (Erlingsson & Brysiewicz, 2017) to address the research questions.In 2011, 369 schools and 12,569 fourth graders in the U.S. participated in TIMSS (Provasnik et al., 2012). Drawing U.S. fourth graders’ performance data from the TIMSS 2011, this study focuses on the information related to geometric shapes and measurement (hereafter referred to as fourth-grade geometry). Specifically, among the 54 geometric items, the 24 released items were analyzed (the latest publicly released items, which can via https://nces.ed.gov/timss/pdf/TIMSS2011_G4_Math.pdf). Half of these items were multiple choices; the other was constructed responses. Information item was used, including item number, item label, cognitive domain assigned by TIMSS (including knowing, applying, reasoning), overall correct percent of U.S. students, and international average (Foy et al., 2013​​). To better understand students' common incorrect choices on the multiple-choice items, Information from "TIMSS 2011 Released Items with Percent Statistics-Fourth Grade" was used (refer to https://timssandpirls.bc.edu/timss2011/international-database.html for more details).

Data analysis

To answer the first research question: What can be learned from the geometric items that U.S. students performed differently, with a focus on understanding the features of these items for supporting learning? Three levels of coding have been done. Firstly, each item was coded for van Hiele levels (The Ohio Department of Education, 2018), and then the items were categorized into three groups. Coding for the van Hiele levels was used to determine the cognitive challenge of each item as stated in the trajectory of geometric progression defined by van Hiele's theory. To establish coding truthfulness, one coder completed the first round of coding independently and then shared the codes with others. There were discrepancies in the codes assigned to six items by coders, and a consensus was attained (Saldaña, 2021).

Once the items were coded for van Hiele levels, this information and the details extracted from TIMSS 2011 on students’ performance data were compiled. This performance data gave us the percentage of students performed each item. This information was compiled into three categories - strong (S) when the U.S. students have a correct percentage of more than 70%, and moderate (M)and weak (W) for percentages between 50%-70% and below 50%, respectively. By comparing the U.S. students’ correct percent with the international average, U.S. students’ performance was further justified by making claims that U.S. students performed weakly in this item but stronger than the national average.

Afterward, each item was carefully read to assess which geometrical concepts were foregrounded in the item. For this process, each coder took turns defining the list of attributes related to each item. The commonalities and discrepancies between coders’ observations were discussed until a consensus was reached (Saldaña, 2021).

To answer the second research question, How do U.S. students perform on each geometry subtopic, and what insights can be gained from the variations in performance regarding assessment for learning? A content analysis method (Erlingsson & Brysiewicz) was followed. Each coder individually coded each item to discern the critical geometric topics as captured in the item. These codes were discussed as a team, and seven specific topics- relative position, line of symmetry, transformation, angle size, connections between 2D-3D shapes, 2D shapes, and measurement- were identified within these 24 items. These geometric topics concerning students' performance data and how students performed on each subtopic of geometry were compiled.

Ethical considerations

Since the data used in this study is derived from a secondary source and is publicly accessible, no Institutional Review Board (IRB) consent was needed. The dataset is publicly available at [https://nces.ed.gov/timss/pdf/TIMSS2011_G4_Math.pdf]. The nature of the data and its public accessibility eliminate the need for individual ethical approval for this analysis.

FINDINGS

U.S. students’ geometric learning strengths and challenges

The first research question is to infer the features of the geometric items for which the U.S. students performed differentially. The international average of correct responses for these items ranged from 15% to 78%, whereas this percentage ranged between 13% and 92% for the U.S. students. Results showed that U.S. students performed strongly (more than 70% accuracy) on nine items, moderately (accuracy percent ranging between 50-70%) on 11 items, and weakly (accuracy percent less than 50%) on five items. The data indicates that U.S. students performed strongly on the items that were either structured in daily contextualized problems or for those that explicitly stated a manipulative expectation (draw, mark, rotate, et al.). Contrarily, they performed moderately for the items that needed students to conceptualize or make connections between geometric ideas. The U.S. students performed poorly for items involving measurement, or that required a deep conceptual geometric understanding (e.g., line of symmetry). A more detailed description of each grouping category is given below.

Items show students’ strength

Table 1 shows that among nine strong-performing items (accuracy percent between 78% to 92%), four items focused on the two-dimensional shape and relative position. These items challenged students cognitively from two major domains: knowing (n = 5) and applying (n = 4). Three items were coded as level 0 on van Hiele levels, and six were coded as level 1. By comparing the U.S. correct percentage with the International Average, the U.S. correct percentage is much higher for these nine items.

In general, the items in the strong category showed that U.S. students performed well on items with explicit details on mathematical manipulation. This claim holds true based on the key descriptors captured from these nine items, like 'rotate,' 'put,' 'order,' 'move,' 'draw,' 'make,' 'tell,' and 'mark.' These items were also designed in contextual settings, i.e., one can relate them to daily situations, such to everyday problem solving like navigating locations in maps (e.g., S2, S8, S9), grounding in a situation similar to video games (e.g., S4), and everyday household items like clocks (e.g., S1).

Items shows students’ potential

Table 2 shows the ten items in the Moderate category (accuracy percent ranging between 50-70%). This category includes items with a range of geometrical concepts, like sizes of angle (M5 and M9), lines of symmetry (M2 and M8), rotation (M3), and reflection (M6). Similar to the Strong category, the items in the Moderate category focused on two cognitive domains: knowing (n = 6) and applying (n = 4). Most of these items are coded under van Hiele’s level 1 (Analysis, n = 9), suggesting that these items have higher cognitive demand. The U.S. correct percent for these ten items is also higher than the International Average.

The items in the Moderate category were more challenging than the items in the Strong category. Most of these items expected students to conceptualize or make connections between geometric ideas. For instance, students were asked to execute 1/2 turn of a given shape/figure (M3), draw an angle between 90 and 180 degrees (M5), identify a right angle (M9), count the number of boxes in the stack (some visible and some invisible; M10). Few items in this Moderate category required students to draw or write responses (e.g., M1, M2, M5, M7).

Items reflect students’ learning challenges

Table 3 shows the five items in the Weak category (accuracy percent less than 50%). These items spanned through the geometrical topics: measurement (n = 3), 2D shape (n = 1) and 2D-3D relation (n = 1); cognitive domains: reasoning (n = 3) and applying (n = 2); and van Hiele’s levels: level 1 (Analysis, n = 3) and level 2 (Informal Deduction, n = 2). These items were challenging for the fourth graders compared to the International Average, especially for four items (W1, W2, W3, and W5). The item wording shows that these items require a deep understanding of the related concepts or procedures. For example, measuring the length of a string (W2), figuring out the perimeter of common shapes (W5), and connecting 2-D and 3-D shapes (W3).

U.S. students’ learning on specific geometric topics

The second research question concerns how U.S. students perform on specific geometric topics. The 24 items were grouped into seven groups, and the following sections discuss each topic area in detail.

Relative position

The data in Table 4 show that U.S. students performed well in finding relative positions in cartesian coordinates. Their correct percentage on these five items ranges from 63% to 92%, much higher than the international average. While analyzing the items, it is interesting that U.S. students’ correct percent dropped rapidly from Item S9 to S8, although the contexts of these two items are the same (see Figure 1; both items offer a map of Lucy's town). The difference is that S9 provides the position (D5) of a building (Lucy's house) and asks students to mark the position on the map, while S8 posit students to tell the position of a building (Correct Responses include H3, (H, 3), 3H, (3, H) or other equivalents)) on the map. These results suggest that U.S. students were familiar with the relative position but needed more directions about reporting a subject's position based on the map.

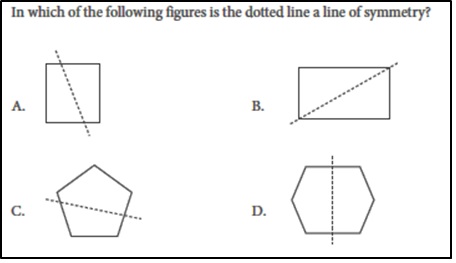
Line of symmetry

Table 5 shows that U.S. students performed strongly on the items related to the line of symmetry compared to the International Average. U.S. students can improve their understanding by solving tasks involving multiple steps and complex shapes. The comparison of the items (Figure 2) substantiates this point. Both items S5 and M8 (Figure 2) fall under the cognitive domains of knowing. 80% of U.S. students identified that option D shows a line of symmetry on the hexagon correctly (S5), while only 66% answered M8 correctly. These results indicated that though students know the concepts of symmetry, they need help to use this knowledge for complex shapes. After zooming in on students' selected options for these two items, data shows that most students answered diagonal(s) as a line(s) of symmetry. Around 14% of students chose option B in S5, suggesting they considered diagonals a symmetry line. Also, 24.2% of U.S. students thought the shape in M8 had four symmetry lines (option D), which might be because these students not only count the horizontal and vertical lines of symmetry on the shape but also count its two diagonals as lines of symmetry. The students who counted diagonals as lines of symmetry might consider that the line of symmetry is a line that divides a shape into two equal parts, regardless of whether these two parts can be folded along into matching parts.

Regarding the second pair of items (S6 and M2 in Figure 2), both require students to draw lines to complete a task; however, students’ performance on M2 was lower than the S6 (see Table 5). It might be because the item wording for M2 was more complex than S6. S6 directly asked them to draw a line of symmetry. However, M2 requires students to create a shape that meets two criteria: have five sides and one line of symmetry. Our analysis reveals that the U.S. students generally were good at the line of symmetry on simple shapes (S6 and S5) but needed help to apply this knowledge to solve the more complicated problems (M8 and M2).

Transformation

U.S. students performed relatively strongly on transformation items (see Table 6), especially on the two rotation items (Item and Item M3 ranked in the top 10). Figure 3 shows the pair of items assessing students' knowledge about rotation. 78% of U.S. students correctly rotated a circular shape 1/4 clockwise (S1), while only 52% correctly identified the position of a flag-like shape after a 1/2 turn (M3). International averages also suggest that M3 is more challenging than S1. One possible reason is that students might be more familiar with clock-like shapes (as given in S1), while the flag-like shape is rare for them daily (M3). Less familiarity with shapes might contribute to their performance on these items.

Regarding items related to reflection, 56% of the U.S. students were able to draw a reflection of the given right triangle (M5). Although this percentage is higher than the international average, tasks that require students to draw may pose additional challenges. Drawing can lead to more errors, particularly if the students' conceptual understanding of reflection is not strong.

Figure 4.

Angle size

Table 7 shows that U.S. students perform well on the three angle-size-related items. Drawing an angle between 90 and 180 degrees (M4) is more challenging than solving multiple-choice tasks (S3 and M9 in Figure 4). S3 and M9 share many similarities (understanding of angle property, angle size, and congruent angles, see Figure 4). Regarding U.S. students' performance on S3 and M9, 78% of U.S. students answered S3 correctly as they answered the ordering of four given angles by size. In comparison, only 68% were able to pick the right angle from the four different angles given (M9). S9 is less challenging for U.S. students as it requires students to visually order four angles positioned in horizontal orientation, whereas M9 asks students first to know what a right angle is and then to pick a right angle from given pictures but in different orientations. There was a 1% performance difference for the international average for S3 and M9; however, this difference was 10 % for U.S. students, indicating that identifying an "abnormal" right angle (based on a different orientation) is a particular challenge for U.S. students.

By examining U.S. students' most incorrect choices on S3 and M9, the data shows that option B in Item S3 and option D in M9 were prominent errors. 14.1% of U.S. students chose option B in S3, which means these students ordered the given four angles from the greatest to least, opposite from the proposed question. More likely, these students may have needed to read the item more carefully. Regarding M9, 24.2% of U.S. students selected option D as the right angle. The underlying rationale of their choice might be because they believe a "right" angle should be horizontally oriented.

2D-3D shape connections

On the topic of 2D-3D shape connections, Table 8 shows that U.S. students performed well on S7 and M1 but failed to do so for W3. W3 (see Figure 5) tests students' knowledge of composing 2-D shapes into common 3-D shapes. 34% of U.S. students identified the correct pattern (option D), while 38% chose option B as the correct option. Such common error suggests that a substantial proportion of U.S. students may know the 2-D components of a cylinder but fail to infer that the length of the rectangle should equal the circumference of the circle, not the rectangle's width.

2D Shapes

Identifying shapes (M6 and W1) is covered in kindergarten; however, it is challenging for all students when the task design is complicated (e.g., Item W1). This is also visible in the percentage of U.S. students and the international average (Table 9). Figure 6 shows Item W1. The core mathematical content of this task is to find the number of sides of given shapes and compare the side lengths. However, the item requires logical thinking as students need to understand the meanings "a shape has four sides, and all sides are not the same length," "a shape does not have four sides and are sides are the same length," and "a shape does not have four sides, and all sides are not the same length." Also, students need to coordinate the picture and the table to report their answers, which might have increased the complexity of the task.

Measurement

Table 10 shows that measurement items were the most difficult for U.S. students. U.S. students got the lowest ranking on W2 and W5 (Figure 7) across the 24 items. W2 asked students to measure the length of a string that is neither a straight segment nor starts at the zero point on the ruler. To solve this item correctly, students must understand the fundamental ideas underlying measurement, know the ruler reading strategies, and mentally unfurl the string. Only one-fifth of U.S. students correctly answered, 9% lower than the International Average. Many U.S. students (33.8%) selected option C, which can be obtained by reading the mark where the string visually ends.

W5 tested students' understanding of perimeter. Typically, students learn the formula or memorize the standard algorithm without grasping conceptual reasoning. To solve Item W5, students need to conceptualize – 'walk all the way around the edge of the square playground' means tracing the perimeter of a square, and 'the length Ruth walk' means the length of the perimeter. Around 43% of U.S. students reported the correct option C, which is 7% lower than the international average. Also, 37% of the U.S. students chose option A, indicating they may lack an understanding of the problem and a deep conceptual understanding of the perimeter or lack experience finding the perimeter of a real-life context.

DISCUSSION

This study is motivated to break the notion that large-scale assessments are often used to rank students’ achievements (e.g., Chen et al., 2021; Mullis et al., 2012; Provasnik et al., 2012; Shapira-Lishchinsky & Zavelevsky, 2020). Guided by the idea of assessment for learning (Small, 2019), this study focused on analyzing the 24 publicly released geometric items in TIMSS 2011 to identify attributes of items that impacted students' performance. This study used content analysis and answered two central questions:What can be learned from the geometric items that U.S. students performed differentially? Moreover, what insights can be gained regarding assessment for learning from the variations in performance across these subtopics? By doing so, this study draws a detailed picture of U.S. students' geometry performance, which can inform nationwide mathematics teachers and curriculum developers with concrete evidence of what and how to make changes to improve students' geometry performance.

Building on students’ strength for learning

Building on children's strengths in geometry can provide children with new learning opportunities (Sinclair & Bruce, 2015). Though there were items for which students' performance was weak, there was a range of items on which they performed well, especially on the items that focused on testing their knowledge about relative locations, lines of symmetry, and transformation. The U.S. students surpassed the international benchmark substantially for most of these items. These findings raise interesting questions, such as whether there are any underlying cultural factors (Izard & Spelke, 2009; Spelke et al., 2010) or curricular strengths (Chen et al., 2009) that support U.S. students' strong performance on some specific topics or types of items? If so, how could educators build on such strengths to empower U.S. students' learning of other subtopics of geometry?

In addition, U.S. fourth graders performed well on the items grouped under level 0 and level 1 of van Hiele Level but struggled with items grouped as level 2. Although having competence at level 0 and level 1 is also an achievement, the field needs to think about possible ways to use guidance from the existing theoretical frameworks to improve students' geometric thinking and performance (Sarama et al., 2021). Building on this observation, large-scale assessments, such as TIMSS, are recommended to include van Hiele Level as a domain of the designed items.

Explore effective approaches to address students’ learning difficulties

Guiding teaching with students’ learning trajectories

Our analysis results highlight that U.S. students struggle most with measurement-related items and require a deep conceptual understanding of geometric concepts or procedures. For example, students seemed to be confused between a line of symmetry and a line that divides a shape into two congruent figures (e.g., S5 and M8, suggesting that students did not conceptually understand the line of symmetry, which allowed them to untangle the confusion). Aligned with Clements and Battista's (1992) early observation that students often use measurement instruments or apply geometric formulas to solve tasks without understanding the conceptual underpinnings, similar situations from the national representative data were observed. For example, only 20% of U.S. students reported the measure of the length of a string that needs to be pulled straight correctly (7cm, W2), but 33.8% of U.S. students (33.8%) selected 8cm, which can be obtained by reading the mark where the string visually ends, suggesting most students lack an understanding of the fundamental ideas underlying measurement.

These observations underscore the importance of deepening students’ conceptual understanding of measurement (Smith & Barrett, 2018). Building on previous literature, Kim et al. (2017) proposed a developmental sequence across the length, area, and volume measurements that reflect students' learning trajectories within the geometrical measurement. Scholars (Clements & Battista, 1986; Lee & Cross Francis, 2016) also have advocated a specific instructional sequence for effective measurement teaching, including "gross comparison of length, measurement with nonstandard units such as paper clips, measurement with manipulative standard units, and finally measurement with standard instruments such as rules" (Clements, 1999, p. 5).

Increasing variation in curriculum

A noteworthy application of a summative assessment strategy within an assessment for learning context is identifying areas where students lack understanding, followed by establishing targets to address these gaps. This study highlights that U.S. students' understanding of geometric concepts needs more depth and flexibility. Despite the items discussed above, the U.S. students needed help with various items requiring them to apply learned knowledge flexibly. For example, about one-fourth of U.S. students recognized an obtuse angle with a horizontal base as a right angle (M9); they failed to recognize the given right angle, which may be because of its nonstandard orientation (Devichi & Munier, 2013; Fuys & Geddes, 1984; Izard & Spelke, 2009; Mitchelmore, 1998;). Although 92% of U.S. students marked the given position on the map correctly (S9), only 87% were able to report the position of the shop on the map (S8). Additionally, most students could correctly rotate a circular shape (S1), but fewer could correctly answer an item asking to turn a flag-like shape (M3).

These findings require further examination of the type of geometrical shapes presented in our curriculum and instruction. The shapes students encounter, either in school or out of school, are often too "perfect" (e.g., equilateral triangle, isosceles triangle, rectangles, and square with horizontal bases), which limits their notions of shapes (also see Aslan & Arnas, 2007; Bernabeu et al., 2021; Clements et al., 1999; Clements & Sarama; Guncaga et al., 2017; Walcott et al., 2009). Similarly, Monaghan (2000, p.192) also concluded that "What emerges is that students (over-)rely on standard representations of shapes as a means of identifying and discriminating between them. It was shown that curriculum materials tend to underpin such perceptions." Thus, examining the type of shapes and tasks used in the curriculum and taught in classrooms is essential. The curriculum and teachers should deliberately introduce shapes with more diverse appearances and orientations to expand students' notions of shapes (Clements & Sarama, 2000; Wang & McDougall, 2019). Promoting teachers’ preparation in teaching geometry might be needed (Kaur Bharaj & Cross Francis, 2020; Steele, 2013; Žilková et al., 2015).

In general, our analysis shows U.S. students had good coverage of a range of geometric topics but struggled to solve more challenging tasks, which aligns with the early observation that the U.S. curriculum prefers to cover an extensive range of topics with limited time to go in-depth which was called "a mile wide and inch deep" (Schmidt & McKnight, 1998). The positive change is that the new Common Core State Standards for Mathematics (CCSSM)(Common Core State Standards Initiative, 2010) have made significant changes, including aligning the new standards with the standards from the top-performing countries and emphasizing the depth of topics and coherence across grade levels (Schmidt & Houang). These changes may lead U.S. students to achieve better on the geometric items in TIMSS. However, researchers (e.g., Zhou et al., 2022) also found that the development of geometry topics in the CCSSM needs to be more coherent and disturbs the learning progression. Thus, examining how the CCSSM responds to our findings of students' strengths and weaknesses in geometry learning and how students performed at TIMSS 2019 will be meaningful.

Informing teacher preparation and professional development

Instead of relying solely on scores from large-scale assessments like TIMSS as a summative evaluation of students' thinking, it is crucial for educational stakeholders to extract valuable insights from this dataset. For example, our analysis has uncovered intriguing aspects of students' geometrical thinking, and these findings should be integrated into teacher preparation programs and professional development settings. This ensures that pre-service and in-service teachers gain valuable insights into student thinking. The central concept behind assessment for learning is not merely to provide a final judgment but to narrow the gap between a learner's current understanding and their desired learning outcomes. To achieve this goal, K-12 teachers should incorporate the nuances of students' conceptions into their interactions as revealed within such assessments, allowing latent thinking patterns to be highlighted during instructional time.

Given that TIMSS data are derived from a diverse pool of students in the United States, it offers a comprehensive overview of students' thoughts that may not be readily apparent in individual states, schools, or students. Thus, similar analysis is recommended to be conducted at different levels. Teachers can adopt these items for specific classrooms as diagnostic items to understand their students' strengths and struggles. Building on this information, teachers can modify their instruction. Meanwhile, teachers can modify these items to develop an assessment of learning (Small, 2019).

Limitation

This study has several limitations. First, it analyzed only 24 released items, whereas TIMSS 2011 included a total of 54 geometry items. Incorporating more items in future analyses could strengthen the study’s findings. Additionally, this study used data from TIMSS 2011 as a case to illustrate how large-scale assessments can be utilized for learning. Future research should consider using updated datasets from 2015 and 2019 to gain a more accurate understanding of current trends and developments in mathematics education. Notably, since 2011 marked the adoption of new curriculum standards in the U.S. (Common Core State Standards Initiative, 2010), using TIMSS 2011 data as a baseline to examine how U.S. students’ performance evolved from 2011 to 2015 and 2019 to understand the impact of these new standards could be a valuable direction for further exploration. Second, this study has done extensive research and taken guidance from the literature to unpack the reasons for students' responses and hypothesized possible misconceptions. Still, the quality of this information can be strengthened by conducting interviews with students and probing into their thinking for the reasons for selecting specific answer choices. Furthermore, this study exemplified the comparison between the performance of U.S. students with the international average; future research could conduct cross-country comparisons. Such comparisons would help evaluate the strengths and weaknesses of students from different countries and provide insights into how curricula across cultures impact student learning.

CONCLUSIONS

Broadfoot et al. (2002) describe assessment for learning as the process of gathering and interpreting evidence to help learners and their teachers determine the learners’ current progress, identify their learning goals, and decide the most effective strategies to achieve them. Simillary, Black et al. (2004) argue that assessments, even those designed of learning, can be used for learning when they provide feedback that informs instructional adjustments to meet learning needs. Drawing on these ideas and continuing our work in studying geometry curriculum (Zhou et al., 2023), this study utilized data from U.S. fourth graders from the TIMSS 2011 assessment, analyzing 24 items qualitatively for learning. The analysis revealed that U.S. students performed well on items involving practical geometrical knowledge but struggled with questions requiring abstract geometrical thinking and reasoning. We also identified a range of potential misconception nationwide, highlighting the importance of enhancing students' conceptual understanding of geometry, particularly in measurement (e.g., length, angle), and their flexibility in applying geometrical knowledge. These findings provide valuable insights for designing tasks that develop students' geometrical thinking and support teachers and curriculum developers in creating targeted instructional tasks. In summary, our study underscores that large-scale assessments, which are often designed of learning, can be creatively utilized for learning, such as guiding professional development, diagnose teaching effectiveness, inform instructional planning, and more. Researchers and educators are also encouraged to replicate this analysis in other mathematical domains across different educational systems to foster meaningful educational improvements. Additionally, stakeholders are urged to make the most of the valuable yet costly data from large-scale assessments to enhance student success.

ACKNOWLEDGMENT

The authors acknowledge the use of data from the Trends in International Mathematics and Science Study (TIMSS) 2011, conducted by the International Association for the Evaluation of Educational Achievement (IEA). The analyses and conclusions in this study are solely those of the authors and do not reflect the views of the IEA or any other organization associated with the administration of TIMSS.

AUTHOR’S DECLARATION