Improving communication, problem-solving, and self-efficacy skills grade-10 students through scientific approach based on discovery learning

Abstract

Education plays an important role in creating a young generation to be able to compete in the era of globalization, one of which is through mathematics learning. The objectives of mathematics learning include mathematical communication, learning to reason mathematically, learning to solve problems, and learning to connect ideas. These abilities are abilities that students must have in facing global challenges. This study aims to determine the improvement of communication skills, the sharpness of mathematical problem solving, and self-efficacy using a scientific approach through the application of the discovery learning model. This study is a quantitative study, and the type of research used in this study is quasi-experimental. The research design used is one group pretest-posttest. This study was conducted in one of the high schools in West Aceh. The study population was 29 grade 10 students. Data collection techniques used test and non-test methods. The findings of the study showed a significant increase in communication skills, problem-solving abilities, and self-efficacy when using the discovery learning approach in the context of trigonometric ratios. The approach is considered quite effective, which means it produces a substantial increase in the cognitive abilities mentioned above among students.

INTRODUCTION

Education is one of the determinants of the advancement or decline of a nation's civilization. Therefore, in this modern era, education plays a crucial role in creating generations capable of keeping up with the rapid development of knowledge, including the field of mathematics [?]). Mathematics is one of the subjects studied at every level of education, from elementary school, middle school, and high school to university. Mathematics also plays an essential role in various other disciplines and serves the function of developing human intellect. Therefore, students must master mathematics as it will enhance their understanding in other fields. Mathematics can be used as a tool, a science, a guiding framework, and also as a form of attitude [?]). Currently, the world has entered the 21st century, also known as the global era, which demands mastery of specific skills. To compete in the global era, students need to become proficient communicators, creators, critical thinkers, and collaborators beyond basic reading, writing, and arithmetic skills ).

The process of mathematics learning is not merely the transfer of knowledge from the teacher to the students, but rather a process conditioned or facilitated by the teacher, so that students actively construct or build their knowledge in various ways. It involves interactions and negotiations between the teacher and students, as well as among students themselves. The intended mathematics education is meaningful, so that students gain something beneficial for themselves after completing the learning process [?]). The National Council of Teachers of Mathematics [?]2000 formulates the objectives of mathematics learning as follows: 1) learning to communicate mathematically (mathematical communication), learning to reason mathematically (mathematical reasoning), learning to solve problems (problem-solving), and learning to connect ideas (mathematical representation). Based on the objectives of mathematics learning, it can be concluded that mathematics education can help students understand concepts, solve problems systematically, relate mathematics to everyday life, and express mathematical ideas effectively both orally and in writing. One of the mathematical abilities that students should possess is mathematical communication skills [?]2018.

Mathematical communication skills are crucial during student discussions, where students are expected to express, explain, describe, listen, inquire, and collaborate to deeply understand mathematics. In short, communication is seen as a way to convey ideas, thoughts, and feelings to others [?]). Furthermore, research conducted by [?]), states that students' mathematical communication skills still yield unsatisfactory results. This is further supported by a research conducted by [?]2021 which mentions that in a discussion with students, the communication is not well-executed, both orally and in writing. Students face difficulties in presenting arguments, even though they have mathematical ideas and concepts in their minds.

In addition to mathematical communication skills, problem-solving abilities are also crucial to be developed in the process of learning mathematics. Problem-solving skills need to be enhanced in mathematics education to improve students' thinking patterns. Students think that by knowing the formula, they can solve problems. However, in reality, it is often found that only a few students who use the 'formula' can successfully find the correct solution. This indicates that students sometimes are unable to solve problems even if they know the formula [?]). If students frequently practice solving mathematical problems and contextual questions, then the mathematical problem-solving skills within the students and the mathematics learning activities become a pattern of good problem-solving habits, leading to the achievement of learning objectives.

In addition to the cognitive domain, students' psychological attitudes in learning also need to be taken into consideration, given that the goal of education in schools is not only to transfer knowledge but also to shape students' behavior and attitudes towards mathematics and its application in daily life. Regarding students' psychological attitudes, there is a psychological aspect closely related to students' problem-solving activities, which is self-efficacy. Self-efficacy is the belief of students regarding their ability to accomplish a task or solve a problem [?]). Besides the influence of individual differences on students' motivation and achievement, self-efficacy is one aspect that can determine whether students succeed or fail in mathematics learning. Self-efficacy is known to affect students' academic motivation, effort, perseverance, and emotional reactions [?]). Having high self-efficacy can encourage someone to continuously attempt to learn and perform tasks, leading to successful task completion [?]).

The research conducted by [?]) serta [?]) also found that the higher the students' self-efficacy, the higher their learning effort. Therefore, students' belief in their own abilities to solve mathematical problems is crucial because without self-confidence, students cannot complete a task optimally. Student-centered learning initiates the learning process with contextual problems. This is because if students can optimize their problem-solving abilities through contextual problems, their learning achievement will also improve. As emphasized by [?]) appropriate learning can enhance the quality of students' mathematical problem-solving skills, leading to improved learning achievement.

One of the learning models that can enhance mathematical communication and problem-solving skills is discovery learning. Discovery learning is a learning model that focuses on providing direct opportunities for active learning for students [?]). According to Bicnell, there are three main attributes of discovery learning, such as: 1) investigating and solving problems to create, integrate, and equalize knowledge, 2) Encouraging students to learn based on their own ways/steps, where students determine the frequency and sequence. 3) Activities to promote the integration of existing knowledge principles as a basis for building new knowledge. In other words, this guided discovery model exposes students to situations where they are free to investigate and draw conclusions, make guesses, use intuition, and engage in trial and error.

The scientific approach is a learning approach designed in such a way that students actively construct concepts, knowledge, laws, or principles through a scientific method [?]2015. The scientific approach means a learning model that focuses on developing students' problem-solving skills and critical thinking in real-life contexts related to the learning concepts [?]). In addition to the scientific approach, the cooperative model is also one of the learning models in which students learn in small groups with different levels of ability. The group learning process encourages students to help each other, fostering a sense of togetherness and unity in achieving common goals [?]).

Based on the description above, this research applies a mathematics teaching strategy using the scientific approach with the discovery learning model for 10th-grade students in high school on the topic of KD 3.8. Generalizing trigonometric ratios for angles in various quadrants and related angles, and KD 4.8. Solving contextual problems related to trigonometric ratios of angles in various quadrants and related angles to support the improvement of communication, problem-solving, and self-efficacy skills.

METHODS

This research is a quantitative research, and the type of research applied in this research is quasi-experiment [?]). The research design used is a one-group pretest-posttest design, aimed at determining the students' competence in mathematics learning on the topic of trigonometric ratios. A one-group pretest-posttest design is used to evaluate the effectiveness of implementing a program [?]2019 [?]2016. The implementation of this research was carried out by [?]2016 in evaluating the influence of stigma on schools in Canada. Before the implementation of the learning process, the students were first given a pretest to assess their initial competence. After the learning process, the students were given a posttest to assess their competence after the implementation of the learning process using the scientific approach with the discovery learning model, which supports communication, problem-solving, and self-efficacy skills. This research was conducted in 10th-grade at SMAN 4 Wira Bangsa Aceh Barat, with a population of 29 students. Based on the presented research design, as shown in Table 1.

The data collection technique in this research employs both test and non-test methods. The problem-solving and communication abilities of students are measured using test instruments, while the self-efficacy of students and the implementation of the applied learning are measured using non-test instruments.

Test Instrument

The test instrument is divided into two parts, namely the pretest and posttest questions. The pretest is used to assess the students' initial knowledge and is administered before implementing the learning model. On the other hand, the posttest is used to measure the students' abilities regarding the taught material and is given after implementing the learning model during the teaching and learning process. In the test instrument, both the pretest and posttest questions are in the form of multiple-choice questions with four answer options.

Instrument Non Test

The non-test instruments consist of self-efficacy questionnaires and an observation sheet for lesson implementation. The self-efficacy questionnaire is divided into pretest and posttest questionnaires, in the form of a Likert scale with 5 response categories. The total items in the self-efficacy questionnaire consist of 15 questions, which are divided into positive and negative statements.

Data analysis techniques used in this research include descriptive statistical analysis, analysis of instrument validity and reliability, normality test, and paired sample t test to test the impact on communication, problem solving, and self-efficacy. Meanwhile, to find out whether communication, problem solving and self-efficacy have increased, the N-Gain Test assisted by IBM SPSS software is used for data analysis. Quantitative data analysis was used to see the magnitude of the increase before and after the treatment by using normalized Gain formula ([?]2020 and the N-Gain value represents an interpretation of the increase in students' communication skills, problem solving and self-efficacy.[?]2019

FINDINGS

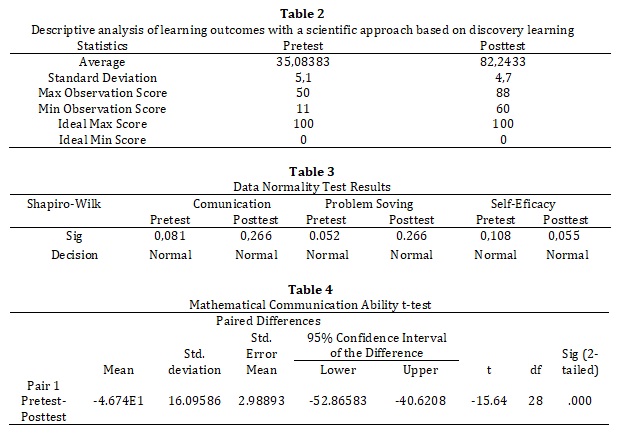
The data obtained in this research are the results of pretests and posttests conducted in grade X at SMAN 4 Wira Bangsa Aceh Barat with a population of 29 students. To assess the students' competencies, the researcher administered a pretest before the instruction and a posttest after the instruction to the participants. This pretest is an assessment of learning outcomes and abilities in communication, problem-solving, and self-efficacy, administered before the mathematics learning process on the topic of trigonometric ratios. On the other hand, the posttest is an assessment of learning outcomes and abilities in communication, problem-solving, and self-efficacy given after the mathematics learning process on the topic of trigonometric ratios. Subsequently, the researcher conducted a trial on the participants. The data obtained were then analyzed. The results of the pretest and posttest are presented in Table 2.

Based on , the average pretest score is 35.08383 with a standard deviation of 5.1, and the average posttest score is 82.2433 with a standard deviation of 4.7. The maximum score on the pretest is 50, while on the posttest, it is 88. The minimum score on the pretest is 11, whereas on the posttest, it is 60. These results indicate that the implementation of mathematics learning processes on the topic of trigonometric ratios using the discovery learning approach has an impact on students' communication, problem-solving, and self-efficacy abilities in grade X. The purpose of this analysis is to evaluate the characteristics of the data obtained after the pretest and posttest.

Hypothesis testing aims to examine the improvement in communication, problem-solving, and self-efficacy abilities after receiving a treatment, compared to before the treatment. The research hypothesis will be tested using the following criteria. Ho is rejected if , and Ho is accepted if , with , which means the average statistical literacy score of students is at least or greater than the Minimum Competency Criteria (MCC) of 70. Next, further testing was carried out to determine significant differences between the pretest and posttest results using the t-test assisted by the SPSS application. Data including normality tests for pretest and posttest scores on communication skills, problem solving and self-efficacy were analyzed using the Shapiro-Wilk test. The following table shows the results of the Paired Sample T-Test carried out in .

Based on the results of the analysis in above, the results show that the pretest and posttest scores for communication skills, problem solving and self-efficacy are normally distributed. Next, t test will be carried out for each ability which will be presented in the table below. In table 4, the significance score of the t-test calculation using SPSS on mathematical communication skills is 0.000 < 0.05. Therefore, it can be concluded that there is a significant difference between the pretest and posttest scores of the mathematical communication taught. using a scientific approach through the Discovery Learning model.

In , the results of the t-test calculation using SPSS show that the significance score for problem solving is 0.000 < 0.05. Therefore, it can be concluded that there is a significant difference between the pretest and posttest scores for problem solving taught using a scientific approach through the Discovery learning model. In Table 6, the significance score obtained from the t test calculation using SPSS is 0.000 < 0.05. Therefore, it can be concluded that there is a significant difference between the pretest and posttest self-efficacy questionnaires taught using a scientific approach through the Discovery Learning model.

Based on the results of the calculation using SPSS, it can be observed that the average increase in N-gain_score is 70.87. Therefore, it can be concluded that there is an improvement in Communication skills through the implementation of the scientific approach using the discovery learning model, categorized as moderately effective, as shown in . Based on the results of the calculation using SPSS, it can be observed that the average increase in N-gain_score is 71.61. Therefore, it can be concluded that there is an improvement in Problem-Solving skills through the implementation of the scientific approach using the discovery learning model, categorized as moderately effective, as shown in .

DISCUSSION

Based on data from research conducted using a scientific learning approach with a discovery learning model on mathematical communication skills, problem solving abilities and self-efficacy, explained in the following discussion.

Mathematical communication abilities of students

The results of calculations using the Paired-Sample T-test assisted by the SPSS application shown in Table 4 show that there are differences in students' mathematical communication abilities before and after learning the trigonometry comparison material using a scientific approach with the Discovery Learning learning model design. This result can be seen from the difference in significant values ​​between the pretest and posttest which is proven by a significance value (2-tailed) of 0.000 (p-value < 0.05) so that the null hypothesis (H_0) is accepted. Apart from that, considering that the average increase in N_gain_score is 70.87, it can be concluded that there has been an increase in communication skills through the application of a scientific approach with the Discovery Learning learning model which is categorized as quite effective. These results are confirmed by research conducted by [?]2020 which shows that the e-module with the discovery learning model is able to increase students' mathematical communication and [?]2017 research which shows that mathematical communication requires clearer descriptions in order to be able to have a positive impact and significant influence on students' mathematics learning. elementary school. In the research conducted by [?]2019, the results showed that the improvement in communication skills and mathematical disposition of students who were taught using the discovery learning model was better than the learning model taught using a conventional approach.

Mathematical problem solving abilities on students

Based on the calculation results of the Paired-Sample T-test with the help of SPSS, it can be concluded that there is a difference in problem solving abilities between before and after learning trigonometry comparisons using a scientific approach through the Discovery Learning model. Based on the analysis results in Table 7, it shows that there is a significant difference between the pretest and posttest results as evidenced by a significance value (2-tailed) of 0.000 (p-value < 0.05) which means the null hypothesis () is accepted. Apart from that , the average score increase in Ngain score is 71.61, so it can be concluded that there is an increase in problem solving skills through the application of a scientific approach with a discovery learning model which is categorized as quite effective. This result is reinforced by research conducted by [?]2019 showing that the problem solving abilities of students taught using the guided discovery model are higher than students taught using traditional learning. The use of discovery learning models can improve junior high school students' mathematical problem solving abilities [?]). [?]2018 discovery learning can help students develop problem-solving abilities through culturally integrated discovery learning.

Mathematical self-efficacy of students

Based on the results of the t test calculations carried out using the SPSS application in Table 6, a significance value of 0.000 ≤ 0.05 was obtained. This means that there is a significant difference between the pretest and posttest self-efficacy questionnaires which were taught using a scientific approach with the Discovery Learning model. This result is strengthened by research by [?]2022 which shows that the discovery learning model can improve students' learning self-efficacy in mathematics learning. Where self-efficacy is a person's ability to produce certain result [?]). [?]2021 interactive learning based on discovery learning can improve students' mathematical representation abilities and self-efficacy. [?]) increasing students' self-efficacy is also one of the positive results of implementing the discovery learning learning model and high self-efficacy can improve abilities. solving students' mathematics problems in Indonesia.

The learning process at SMA Negeri 4 Wira Bangsa, using the scientific approach with the discovery learning model, makes students more enthusiastic and cohesive in participating in classroom activities. Before the teacher enters the classroom, students have already taken their seats neatly and prepared their writing tools and books. During the learning process, students appear enthusiastic and actively engaged. They can participate in discussions and exchange opinions with their groups to arrive at answers and conclusions related to the taught material, specifically the topic of trigonometric ratios. Students are also capable of presenting their findings in front of their peers. The teacher's role is mainly to supervise the students during the learning process. During the learning process, if there are students who have questions or difficulties understanding a certain topic, their peers will be the ones to answer those questions. This activity allows students to interact with each other to reexplain the concepts taught by the teacher and to solve problems given by the teacher using appropriate and correct steps. Additionally, it enables them to tackle mathematical problems, thus enhancing students' abilities in communication, problem-solving, and mathematical self-efficacy.

The research results of [?]) demonstrate that the discovery learning model is effective in enhancing students' learning achievement and self-efficacy in mathematics education. Self-efficacy plays a crucial role in improving students' learning achievements in mathematics; thus, mathematics professors or teachers need to pay attention to psychological factors that can influence students' self-efficacy in mathematics education. By implementing the discovery learning model and paying attention to these factors, it is expected to improve the quality of mathematics education and students' learning achievements in the future. This research aligns with the findings of [?]) which show that the implementation of guided discovery learning model has an influence on students' mathematical problem-solving skills. The research results of [?]) indicate that the improvement of communication skills taught through discovery learning is better than those taught through conventional approaches. Moreover, there is no interaction between the discovery learning model and the students' level in enhancing mathematical communication skills. Therefore, mathematics teachers can apply the guided discovery learning model in teaching the construction of polyhedra in the future. The findings of [?]2014 research indicate that different mechanisms underlie guided discovery learning and problem-solving prior to instruction: in guided discovery learning, the discovery mechanism is inherent in the method itself. On the contrary, the effectiveness of problem-solving prior to instruction does not rely on students' discovery of canonical solutions, but on the cognitive processes related to problem-solving, which prepare students for a deeper understanding during subsequent instruction.

CONCLUSIONS

The finding concluded that there was an influence of applying a scientific approach with the Discovery Learning model on the topic of trigonometry comparisons for class SMAN 4 Wira Bangsa Aceh Barat on mathematical communication skills, problem solving, and students' self-efficacy before and after the learning process. It is hoped that further research can be carried out to develop other skills that students must have in other subjects and mathematics teachers are expected to be able to design mathematics learning practices using innovative learning approaches to facilitate improving student competence.

ACKNOWLEDGMENT

The author would like to thank all participants in this study. their kind and selfless collaboration would like to thank all participants in this research who have collaborated well and selflessly in completing this research.

AUTHOR’S DECLARATION